Blender Python #0002

By telleropnul, March 12, 2020

Terminology

Origins

There are only 2 origins:
World origin (0,0,0) in the Global coordinate-system.
Object origin for each object.  You can place the object origin anywhere, even ‘outside’ of the object.

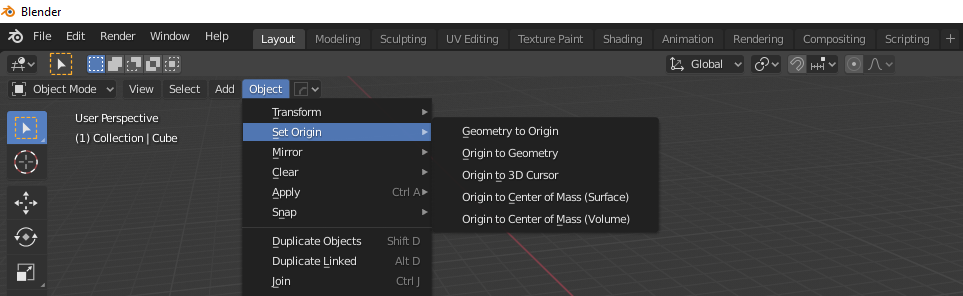
If you go into Edit mode, an object’s origin is….well….the origin, and therefore (0,0,0). Vertices coordinate  values are always relative to the object’s origin.

Global versus Local

This brings us to coordinate-systems.  Suppose that I had two spheres. Each one obviously has a different position in “the world,” that is to say, in the global coordinate-system.

Now suppose that I am working on one sphere individually.  The frame-of-reference that I am interested in now concerns only that sphere, irrespective of “where in the world” it may now be. I might want to position the cursor to “the center” (0,0,0) of that sphere, which has nothing at all to do with “where in the world” that sphere is. So, I’m now speaking in the “local” coordinate system of that particular sphere.

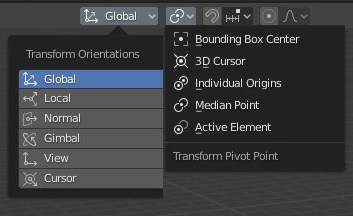
Coordinate systems are also called Transform Orientations.  A coordinate system is about the orientation of X/Y/Z axes.

Pivot

Pivot or Transform Pivot Point  has nothing to do with coordinate systems nor setting an object’s origin.  This is simply which origin to use as the pivot for a transform (move, rotate, scale) or modifier.  For an operation on a single object we will want the operation to perform relative to the object’s origin.  For multiple objects, the default is Median Point (= average of all object’s origins).

Keyboard shortcuts

G, R, S will move (= ‘translate’), rotate, scale along world (=Global) axes.
GG, RR, SS will move, rotate, scale along edit mode (= Local) axes.

When you use the wrong frame-of-reference

The purpose of the following piece of code is to move an object’s origin to its bounding box center.
Note that for a heavily modified object, it’s origin likely no longer sits in its “center of mass (volume).”

Example 1 (incorrect)

1
2
3
4
5
6
7
8
9
10

import bpy
from mathutils import Vector, Matrix
 
obj=bpy.context.active_object
center = 0.125 * sum((obj.matrix_world @ Vector(bound) for bound in obj.bound_box), Vector())
obj.location = center
obj.data.transform(Matrix.Translation(-center))
obj.data.transform(Matrix.Scale(0.998, 4, Vector((-1, 0, 0)) ) )
obj.data.transform(Matrix.Scale(0.998, 4, Vector((0, -1, 0)) ) )
obj.data.transform(Matrix.Scale(0.998, 4, Vector((0, 0, -1)) ) )

Example 2 (correct)

1
2
3
4
5
6
7
8
9
10
11

import bpy
from mathutils import Vector, Matrix
 
obj=bpy.context.active_object
center = 0.125 * sum((Vector(bound) for bound in obj.bound_box), Vector())
obj.location = obj.matrix_world @ center
obj.data.transform(Matrix.Translation(-center))
 
obj.data.transform(Matrix.Scale(0.998, 4, Vector((-1, 0, 0)) ) )
obj.data.transform(Matrix.Scale(0.998, 4, Vector((0, -1, 0)) ) )
obj.data.transform(Matrix.Scale(0.998, 4, Vector((0, 0, -1)) ) )

obj
Contains the active object.
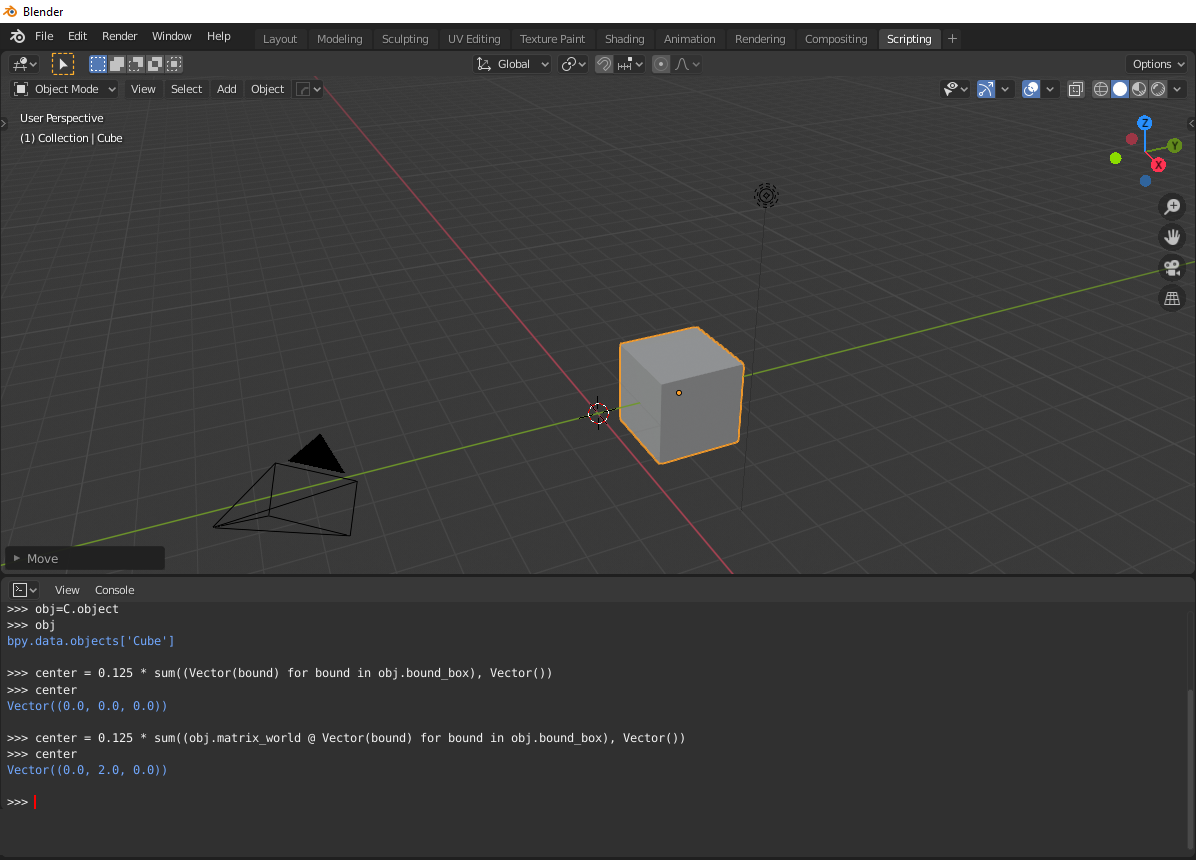
center
Does the following: for each vertex in the bounding box (8x), sum the coordinates and divide by eight.  This results in the coordinates for the bounding box center (vertex).  Very clever.  Frame-of-reference should be the object’s local space.

For our simple cube, the bounding box center expressed in local coordinate-system coordinates coindices with the object origin = (0,0,0)

obj.matrix_world @
This Math helper function takes (local) coordinates and expresses them in their world space equivalent e.g. relative to the world origin (0,0,0).

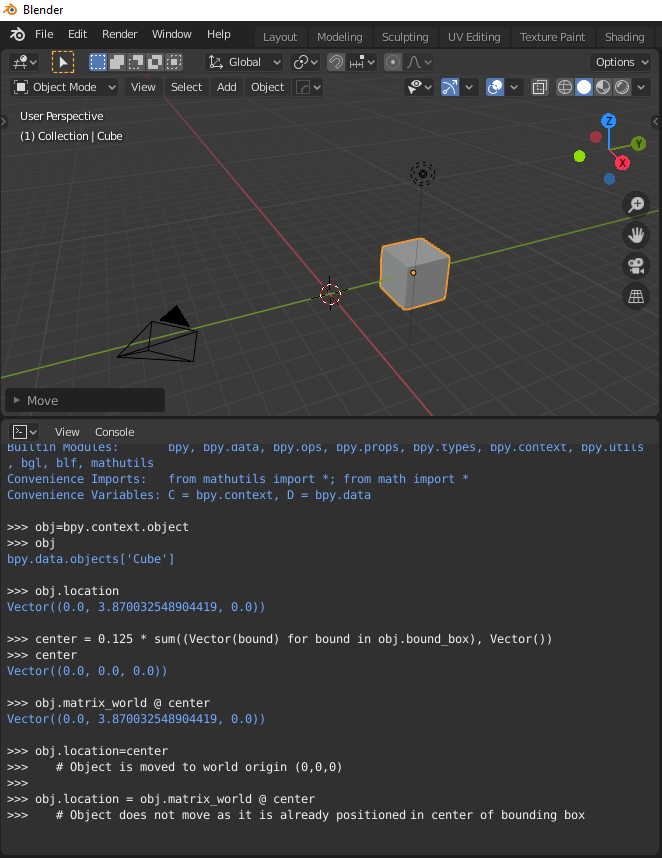
obj.location
Position of an object in world space.  (X,Y,Z) coordinate values are numbers relative to world origin.
obj.location=center
We don’t want to do this here.  Remember center is expressed in local coordinate-system.  It would move the cube to the world origin (0,0,0) which is not what we want.
obj.location=obj.matrix_world @ center
The object’s bounding box center coodinates are expressed using the global coordinate system.

Apply transforms 

Applies several transformations to the selected objects. The object transformation coordinates are transferred to the object data. If the objects have hierarchical descendants, it also applies those transformations to their children.

Applying transform values essentially resets the values of object’s position, rotation, or scale, but does not actually do anything to the object. The object origin point is moved to the global origin and the transform values are set to zero. In terms of scale, the scale values return to 1.

obj.data.transform(Matrix.Translation(-center))
‘Same as ‘apply translation’  X, Y and Z position values are now set to zero without the object moving.

The object local origin is set to the world origin and local space coordinates values (… , … , …) for each of the object’s vertices will be incremented / decremented to suit.  The object transformation coordinates are transferred to the object data.